برنامهی تشخیص عدد اول در پایتون

اعداد اول یکی از مفاهیم پایهای و مهم در علم ریاضیات هستند که در بسیاری از زمینههای علمی و فنی استفاده میشوند. تشخیص اعداد اول یکی از مهارتهای اساسی در برنامهنویسی است که میتواند به شما در حل مسائل مختلف و بهبود تفکر محاسباتی کمک کند.
در این مقاله، به شما یاد خواهیم داد چگونه با استفاده از زبان برنامهنویسی پایتون، برنامهای ساده بنویسید که قادر به تشخیص عدد اول در پایتون باشد. با دنبال کردن این مقاله، قدم به قدم خواهید آموخت که چگونه الگوریتمهای ابتدایی ریاضی و برنامهنویسی را ترکیب کنید تا برنامهی کارآمدی برای تشخیص اعداد اول ایجاد کنید.
اگر تازهوارد هستید و میخواهید از پایه با زبان پایتون آشنا شوید، پیشنهاد میکنیم به دورهی آموزش پایتون مراجعه کنید.

معرفی اعداد اول و اهمیت تشخیص آنها
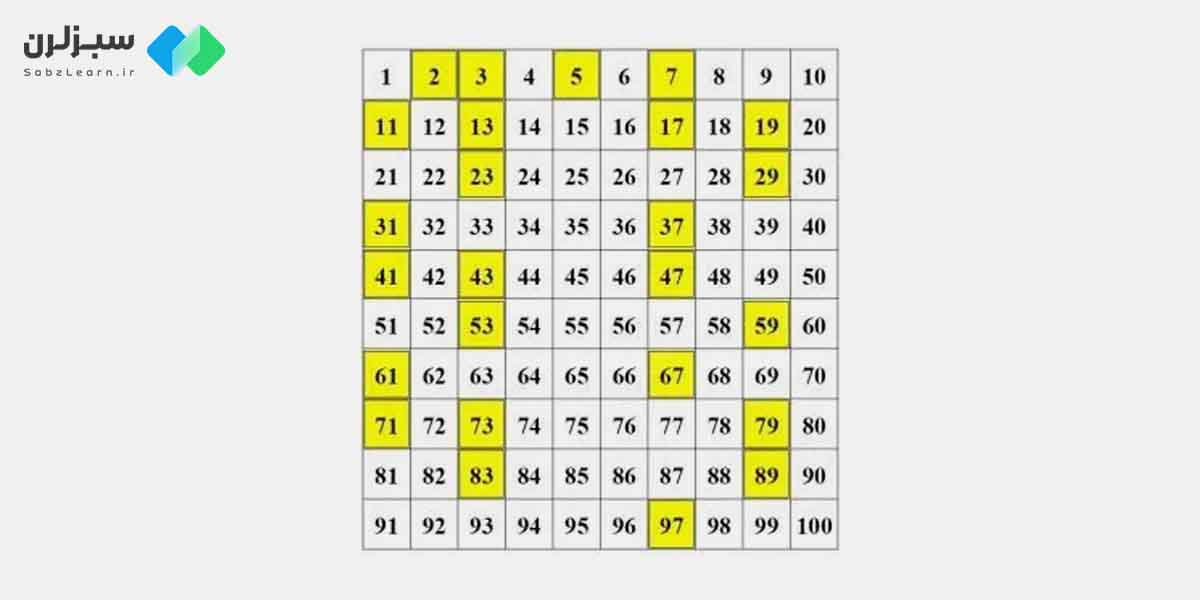
اعداد اول اعدادی هستند که تنها به خودشان و عدد یک قابل تقسیم هستند. به عبارت دیگر، اعداد اول اعدادی هستند که فقط دارای دو مقسوم علیه، یعنی 1 و خود عدد هستند. برخلاف اعداد کامل که بیشتر از دو مقسوم علیه دارند، اعداد اول تنها دو مقسوم علیه دارند که این ویژگی آنها را از سایر اعداد متمایز میکند.
تشخیص اعداد اول از اهمیت ویژهای برخوردار است، زیرا استفاده از این نوع اعداد در بسیاری از الگوریتمها و مسائل ریاضی و کامپیوتری ضروری است. از جمله کاربردهای اعداد اول میتوان به رمزنگاری اطلاعات، بهینهسازی الگوریتمها، و حتی تولید اعداد تصادفی اشاره کرد.
بنابراین، شناخت و تشخیص اعداد اول نه تنها برای تقویت مفاهیم ریاضیاتی ما بلکه برای بهبود تواناییهای برنامهنویسی و حل مسائل مختلف از اهمیت بالایی برخوردار است.
الگوریتمهای تشخیص اعداد اول
الگوریتمهای تشخیص اعداد اول یکی از موضوعات مهم در علوم کامپیوتر و ریاضیات است. این الگوریتمها برای بررسی اینکه آیا یک عدد خاص اول است یا خیر، استفاده میشوند. در زیر یک الگوریتم ساده برای تشخیص اعداد اول آورده شده است:
الگوریتم تشخیص اعداد اول:
1 | برای تشخیص اعداد اول، ابتدا عدد مورد نظر را بررسی میکنیم.
2 | اگر عدد کمتر از 2 باشد، آن را به عنوان “عدد اول” در نظر نمیگیریم، زیرا تعریف اعداد اول از 2 شروع میشود.
3 | برای بررسی اینکه آیا عدد قابل تقسیم بر اعدادی غیر از 1 و خودش است، از یک حلقه تکرار استفاده میکنیم.
4 | حلقه از 2 تا جذر عدد مورد نظر اجرا میشود و هربار عدد را بر تمامی اعداد از 2 تا جذر عدد چک میکنیم.
5 | اگر عدد بر تقسیم بر اعداد دیگری بدون باقیماندن باشد، آن را به عنوان “عدد اول” تشخیص میدهیم. در غیر این صورت، آن را به عنوان “عدد غیر اول” در نظر میگیریم.
6 | پس از خاتمه حلقه، اگر هیچ عددی پیدا نشده که تقسیمپذیری عدد را نشان دهد، آن را به عنوان “عدد اول” تشخیص میدهیم.
الگوریتم بالا یکی از سادهترین الگوریتمها برای تشخیص اعداد اول است و برای اعداد کوچک به خوبی کار میکند. البته برای اعداد بزرگتر، الگوریتمهای پیچیدهتر و بهینهتری نیاز است که با استفاده از اصول ریاضی و الگوریتمی مانند (sieve) اعداد اول را به صورت سریعتر و کارآمدتر تشخیص میدهند.
پیشنهاد دوره: آموزش پایتون
برنامهنویسی به روش جستجوی اعداد اول
برنامهنویسی به روش جستجوی اعداد اول یک موضوع جالب و مفید است. در این روش، ما به دنبال اعداد اول در یک بازه خاص از اعداد هستیم و برنامه را طوری طراحی میکنیم که این اعداد را شناسایی کند. این روش میتواند برای اعداد بزرگ بهینه نباشد ، اما برای مقادیر کوچک و تمرینی بسیار مناسب است.
یک نمونه کد ساده به زبان Python برای جستجوی اعداد اول در یک بازه مشخص را در زیر میآورم:
```
python
def is_prime(num):
if num < 2:
return False
for i in range(2, int(num**0.5) + 1):
if num % i == 0:
return False
return True
def find_primes_in_range(start, end):
prime_numbers = []
for num in range(start, end+1):
if is_prime(num):
prime_numbers.append(num)
return prime_numbers
start_range = 1
end_range = 50
primes_in_range = find_primes_in_range(start_range, end_range)
print(f"Prime numbers in the range {start_range} to {end_range}: {primes_in_range}")
```
این کد از دو تابع استفاده میکند. تابع اول، `is_prime`، بررسی میکند که آیا یک عدد مشخص اول است یا خیر. تابع دوم، `find_primes_in_range`، تمام اعداد اول در یک بازه مشخص را پیدا میکند و در یک لیست ذخیره میکند. در نهایت، اعداد اول در بازه مشخص چاپ میشوند.
برنامهنویسی به روش استفاده از Sieve
برنامهنویسی به روش فیلتر ارولا (Sieve of Eratosthenes) یک روش بسیار کارآمد برای جستجوی و شناسایی اعداد اول است. این روش به ما امکان میدهد تا با استفاده از یک آرایه یا لیست، تمام اعداد اول تا یک حداکثر تعیین شده را شناسایی کنیم.
در این روش، ابتدا یک آرایه یا لیست اعداد از 2 تا یک عدد حداکثر مشخص شده ایجاد میکنیم. سپس اعداد غیر اول را به یک ترتیب خاص حذف میکنیم تا در نهایت تنها اعداد اول باقی بمانند.
یک نمونه کد ساده به زبان Python برای جستجوی اعداد اول با استفاده از روش فیلتر ارولا به شرح زیر است:
```
python
def sieve_of_eratosthenes(max_num):
primes = []
is_prime = [True] * (max_num + 1)
is_prime[0] = is_prime[1] = False
for num in range(2, int(max_num ** 0.5) + 1):
if is_prime[num]:
for multiple in range(num * num, max_num + 1, num):
is_prime[multiple] = False
for num in range(2, max_num + 1):
if is_prime[num]:
primes.append(num)
return primes
max_number = 50
primes_list = sieve_of_eratosthenes(max_number)
print(f"Prime numbers up to {max_number}: {primes_list}")
```
در این کد، تابع `sieve_of_eratosthenes` اعداد اول تا یک حداکثر مشخص را شناسایی میکند و در یک لیست ذخیره میکند. سپس این اعداد چاپ میشوند.
پیشنهادات برای بهبود کدها
بیایید چند پیشنهاد برای بهبود کد و افزایش عملکرد آن را بررسی کنیم:
1 | بهبود عملکرد تابع
برای اعداد بزرگتر، محاسبه جذر ممکن است زمانبر باشد. بهتر است از روشهای بهینهتری برای بررسی اعداد اول استفاده کنید. برای مثال، میتوانید از روش Sieve ارایه شده در قدرت بخشیدن به اعداد برای این منظور استفاده کنید.
2 | بهبود خروجی
در حال حاضر، خروجی کد فقط یک جمله از اینکه آیا عدد اول است یا نه، است. میتوانید خروجی را به شکل یک لیست اعداد اول یا غیر اعداد اول تغییر دهید.
3 | مدیریت موارد خاص
در حال حاضر، کد شما ممکن است با ورودیهای نامناسب به خطا برخورد کند. بنابراین، مهم است که شرایط ورودی را دقیقاً بررسی کرده و مدیریت مناسب برای انواع ورودیهای مختلف اعمال کنید تا از بروز خطاها جلوگیری شود.
4 | تست واحد (Unit Testing)
تست واحد یک فرایند آزمون است که در آن هر بخش یا واحد از کد شما به تنهایی و جداگانه توسط یک تست مورد آزمون قرار میگیرد. هدف اصلی از تست واحد، اطمینان حاصل کردن از صحت و عملکرد صحیح هر بازه کوچک از کد است. این بازه معمولاً یک تابع، متد یا کلاس مشخص است.
با اعمال این پیشنهادات، میتوانید عملکرد کد خود را بهبود بدهید.
نتیجهگیری
در این مقاله به ساخت برنامهی تشخیص عدد اول در پایتون پرداختیم و روشها متنوعی برای ساخت این برنامه استفاده کردیم همچنین پیشنهاداتی برای بهبود عملکرد برنامه ارائه دادیم تا پروژه خود را توسعه دهید؛ اگر هر مشکلی یا سوالی درباره این پروژه داشتید در بخش نظرات آن را مطرح کنید.




نظری برای این مقاله ثبت نشده است